
Shape Control of Tendon-Actuated Tensegrity Structures, M.S. Thesis Defense
Abstract:
As we further extend our reach into outer space, there exists an unmet need for autonomous agents to carry out highly dexterous manipulation tasks such as on-orbit servicing and habitat construction. To be packaged efficiently for transport and autonomously deployed at a remote destination, these robotic mechanisms must be lightweight, yet highly articulated. Tensegrity structures, which comprise a continuous tendon network, are a suitable candidate for carrying out dexterous manipulation tasks in outer space. This thesis presentation focuses on controlling the shape of tensegrity structures by changing the tension in the supporting tendons.
A vector-based approach is used to model the multi-body dynamics of tensegrity structures in a non-minimal coordinate system. This methodology is further extended to handle Class-k structures by modeling bar contact forces as Lagrange constraint forces. Leveraging the vector-based dynamics model, a state feedback controller is developed to regulate the shape of a tensegrity structure to a desired reference trajectory.
The developed control law is implemented in simulation on several Class-1 and Class-k tensegrity structures. Then, a novel robotic manipulator is developed by using self-similar iterations to yield a structure that is both highly dexterous and lightweight, proving that the modeling and control framework can be used to design complex engineering structures. Finally, an experimental cylindrical triplex tensegrity structure is constructed and actuated based on the methods described. Through an open-loop demonstration, it is shown that the experimental structure serves as a suitable basis for testing future tensegrity control architectures.
Nov.
2021
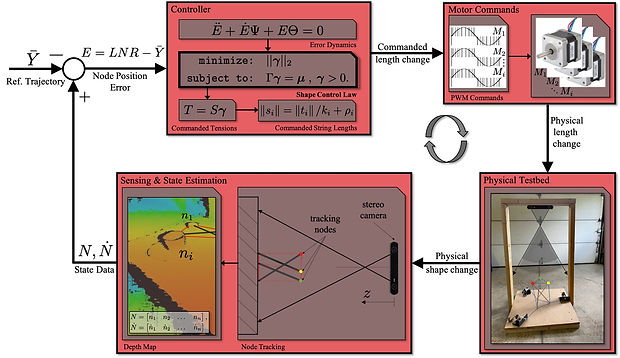
Model-based Control of Tendon-Actuated Tensegrity Robots
Summary:
-
This presentation focuses on controlling the shape of tensegrity structures by changing the tension in the supporting tendons. System dynamics are formulated as a second-order matrix differential equation to improve the accuracy of numerical computations by exploiting the tensegrity’s mathematical structure. Then, state feedback is used to regulate node positions by solving for tendon force densities in a linear programming problem. A novel robotic manipulator is introduced to showcase the capability of this approach.

Apr.
2021
Towards Optimal Control of Tensegrity Structures
Summary:
-
Traditional robotic manipulators comprise a set of rigid members that are connected at mechanical joints. For these limited degree-of-freedom structures, actuator failure could mean the loss of key maneuverability. Tensegrity systems, on the other hand, are defined as a set of compressional elements that can be equilibrated by an internal tension network. This allows the designer to choose a tension topology that optimizes a number of different parameters such as maneuverability and stiffness. By articulating the tensegrity's tensional elements, it becomes possible to change the overall shape of the structure. Tensegrity shape control has been studied using model-based and data-based techniques. However, an optimal shape control law is yet to be realized. In this presentation, I summarize my initial findings on tensegrity structures and provide a brief example of the optimal control of space structures.
Apr.
2020
Foundations of Optimal Control
Summary:
-
In these progress reports, I lay the groundwork for optimal control of tensegrity structures by reviewing the LQR control strategies that were used to stabilize the Draper RPL model.